Fluid structure interaction (FSI) is the interaction of static, moving, or deformable structural components with a fluid flow. FSI is one of the most important examples of multi-physics problem solving. FSI has wide-ranging applications, ranging from large-scale problems such as the dynamic instability of a bridge subject to a strong wind, to small-scale problems such as the flow of blood through a heart valve.
When FSI occurs, fluid flow deforms a physical structure. The deformation of the structure in turn changes the fluid flow. Traditional fluid flow simulation does not account for the deformation interaction. Such simulations will at least be incomplete. At worst, they will be misleading and may well not show up a problem which could have catastrophic consequences. Without FSI analysis, the resulting product may not perform as expected, and costly and time-consuming redesigns may be necessary. FSI simulation allows the interactions between fluids and structures to be predicted, enabling engineers to visualise and optimise the behaviour of complex products with the highest confidence. The engineering team can investigate complex engineering problems in depth and gain a much better understanding of their product’s behaviour.
The physical theory behind FSI can be very complex. In providing the following example of an FSI analysis, we have selected a simple example where the trend of results could be arrived at intuitively. However, you will see that FSI provides a level of detail unlikely to be matched by any physical experiment. For this sample analysis, we will apply FSI to the blade coating process.
The blade coating process
Blade coating (also known as tape casting, knife coating, or doctor blading) is an established low cost ceramic forming technique for the manufacture of large areas of ceramic tapes and sheets. In the 1940s, blade coating was introduced as a method of producing thin sheets of piezoelectric ceramics and capacitors. Today, the technique is widely used in the production of many different devices, e.g. electronic substrates, multilayer ceramic packages, polymer batteries, photovoltaics, or electrodes for molten carbonate fuel cells. Films as thin as 5 micrometers can be produced using blade coating. A typical blade coater is shown in Figure 1.
In cases where the desired coating thickness and quality is difficult to achieve experimentally, a numerical simulation of the process would clearly be advantageous. Simple numerical models have been used for some years, but these have mostly been limited to two dimensional (2D) studies. As discussed in [4], these earlier models could not predict three dimensional flow effects, nor consider any effects caused by flexing of the blade. The author now contends that 3D modelling is feasible.
Our 3D analysis and modelling of the blade coating process combines Fluid Structure Interaction (FSI) analysis and multi-phased Volume of Fluid (VOF) analysis. Combining the two approaches allows the whole coating process to be simulated in three dimensions. With the animated 3D results, we can study the lateral behaviours of the slurry and the blade, and the quality of thin film along the two sides. Our 3D numerical approach enables complex coating processes to be studied at a level of detail not previously possible.
While a more detailed discussion of the 3D analysis and modelling of the coating process follows, for a quick overview of what can be achieved through numerical modelling please view the animations and better quality diagrams here.
Example machine configurations analysed
For this example, two typical types of blade coating techniques are analysed. One with a reservoir and one without. For simplicity, we will consider the machine configuration where the substrate is static and the blade/reservoir moves at with constant speed. These configurations are illustrated in Figures 4 and 5. For further simplicity of explanation, we will also assume that the fluid is Newtonian (constant viscosity coefficient), and that other parameters such as the blade gap and blade thickness are constant. In practice, the method can be applied to non-Newtonian, porous, compressible, and power-law fluids and to variable machine configurations and material parameters.
Figure 4: Principle of blade coating using blade/frame only. The frame is moving and coating liquid along the substrate (top image). Wet layer thickness is controlled by the gap between the blade and the substrate (bottom image).
Figure 5: Principle of blade coating using a reservoir which stores a sufficient amount of slurry. The tank with blade at the front is moving along the substrate to coat a wet film.
Example material properties
In this analysis, the coating blade is made of standard steel and the CL3000 slurry is chosen. Their respective material properties can be found in Table 1.
| Properties | Steel blade | CL3000 slurry | Air |
|---|---|---|---|
| Density (g/mm^3) | 7.80×10^-3 | 3.80×10^-3 | 1.02×10^-6 |
| Young’s modulus (N/mm^2) | 2.10×10^5 | --- | --- |
| Poisson ratio | 0.30 | --- | --- |
| Viscosity (N/mm^2-ms) | --- | 3.15×10^-3 | 1.51×10^-8 |
| Coefficient of tension (N/mm) | --- | 3.55×10^-5 | 0.00 |
| Atmospheric pressure (N/mm^2) | --- | --- | 0.101 |
Simulation setup
Fluid meshing and boundary conditions (FSI = Fluid Structure Interface)
Initial conditions of slurry
Structure meshing and boundary conditions
Simulation results and discussions
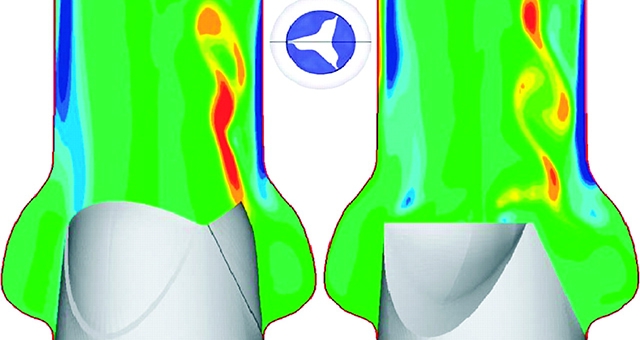
Nodal pressure distribution of the slurry
Case 1: The difference between the maximum and minimum stresses is not significant.
Case 2: Although the fluid near the bottom of the blade has higher pressure than that of the rest, the difference is not significant.
Z-level of the slurry
Case 1: The wet film’s thickness varies across the longitudinal (Y) and lateral (X) axes. Slurry level at the middle is higher than the surrounding edges.
Case 2: The wet thickness is quite consistent along the substrate when the slurry level in the tank is sufficient.
Case 1: The slurry does not adhere well onto the substate starting very early in the process.
Case 2: The slurry distribution becomes inconsistent towards the end of the process when there is insufficient fluid left in the tank.
Bottom adherence
Structural stress distribution
Comments on simulation results
- Case 2 produces wet layer more consistently than Case 1.
- Case 1 has relatvely larger void at the bottom than that of Case 2.
- Insufficient level of slurry in the reservoir leads to inconsistent slurry distribution, better results can be obtained for Case 2 if the reservoir is being constantly filled up during the process.
In summary, simulation results show the distintive characteristics and outcomes of the two processes. While Case 1 has simplier configurations, the resulting slurry quality is not as good as that of Case 2.
The benefits of FSI simulations
The example analyses demonstrate that the combination of FSI and VOF techniques delivers both precise and visually illuminating solutions to complex multiphysic and multiphasic problems. Even the most expensive of physical experiments are unlikely to present solutions with similar precision and clarity.
Similar numerical simulations can be used to predict the behaviours of both multiphase and power-law fluid and flexible structures. Detailed results such as stress, displacement, liquid distribution, wall adherence and velocity can be easily visualised and analysed. For coating machine manufacturers, the application of these simulation techniques can reduce machine development costs and development time.
In a similar manner, these techniques can be applied to problem solving in many other areas of applications, of which a few examples follow:
How CAEbay can help
CAEbay is an experienced engineering and computer simulation company, offering insightful engineering analysis and computer simulations for a wide variety of applications. For a no-obligation review of your engineering and development needs or problems, please email info@caebay.com.
References:
[1] http://www.mtixtl.com. Accessed on 30 Oct 2017.
[2] Jabbari M., Bulatova R., Tok A.I.Y., Bahl C.R.H., Mitsoulis E., and Hattel J.H. (2016). Ceramic tape casting: A review of current methods and trends with emphasis on rheological behaviour and flow analysis. Materials Science and Engineering B, 212, 39–61.
[3] https://commons.wikimedia.org. Accessed on 30 Oct 2017.
[4] Wonisch A., Polfer P., and Kraft T. (2011). A Comprehensive Simulation Scheme for Tape Casting: From Flow Behavior to Anisotropy Development. Journal of the American Ceramic Society, 94 (7), 2053–2060.
[5] Jabbari M., Pryds N., and Hattel J.H. (2014). Modelling of Tape Casting for Ceramic Applications. Department of Energy Conversion and Storage, Technical University of Denmark.
[6] Hirt C.W. and Nichols B.D. (1981). Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. Journal of Computational Physics, 39, 201-225.
Acknowledgements. The author would like to thank Cliff Walker of Vacmobiles.com for his insightful comments and suggestions that greatly improved the quality of this note. Any errors that remain, of course, are the author’s own.
Copyright. CAEbay endeavours to contribute its knowledge towards engineering progress. This note is free for any use, either commercial or educational, that could make products better and safer. However, if published elsewhere, acknowledgement of the source would be much appreciated.
Disclaimer of reliability. The information in this note is correct to the best of our knowledge. However, because material supply and manufacturing quality are outside our control, all recommendations are made without guarantee on the part of the author or CAEbay. The author and CAEbay disclaim any liability in connection with the use of this information.
Feedback or queries on this note? We are keen to improve the accuracy and value of CAEbay’s notes. If you have any feedback or queries, please email info@caebay.com. We would be pleased to hear from you!